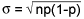as the
binomial distribution.
The Central Limit Theorem says that as n increases, the binomial
distribution with n trials and probability p of success gets closer
and closer to a normal distribution. That is, the binomial
probability of any event gets closer and closer to the normal
probability of the same event. The normal distribution has the same
mean μ = np and standard devia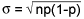tion as the
binomial distribution.
You can use the sliders to change both n and p. Click and drag a slider with the mouse. Start by choosing p. The binomial distributions are symmetric for p = 0.5. They become more skewed as p moves away from 0.5. The bars show the binomial probabilities. The vertical red line marks the mean np. The red curve is the normal density curve with the same mean and standard deviation as the binomial distribution. As you increase n, the binomial probability histogram looks more and more like the normal curve.